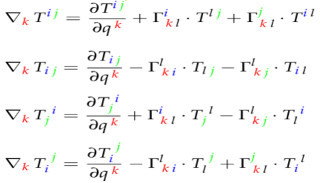Angewandte Mathematik für Ingenieure
Ausgewählte Kapitel der Mathematik
Videos zu ausgewählten Kapiteln der Mathematik
Zahlentheorie
In dieser Rubrik Ausgewählte Kapitel der Mathematik möchte ich Ihnen hier einige Gebiete aus der Zahlentheorie bereitstellen, die sich in erster Linie an Studierende aus dem Fachbereich Informatik richten, aber auch an alle diejenigen, die sich für Fragestellungen aus der Zahlentheorie interessieren.In den ersten Videos werden zunächst einige Grundlagen aus der elementaren Zahlentheorie erarbeitet, für deren Einsicht man hier mit einfachsten mathematischen Hilfsmitteln, so wie sie in etwa in der Schule gelehrt werden, auskommt. Dazu gehören unter anderem:• Teilbarkeitseigenschaften der ganzen Zahlen,• Satz vom kleinsten Teiler,• Satz von Euklid über die Anzahl der Primzahlen,• Hauptsatz der elementaren Zahlentheorie,• Primzahlen und das Sieb des Eratosthenes,• kleiner Satz von Fermat,• Pseudoprimzahlen und Carmichaelzahlen,• Verteilung der Primzahlen und die Primzahlzählfunktion,• Division mit Rest,• Mersenne-Primzahlen und der Lucas-Lehmer-Primzahltest,• modulare Addition, modulare Multiplikation.
Neben der elementaren Zahlentheorie werden desweiteren auch noch einige interessante Themen aus der analytischen Zahlentheorie behandelt, die sich insbesondere Methoden aus der höheren Analysis und der Funktionentheorie bedienen. Im Großen und Ganzen werden in der analytischen Zahlentheorie Konzepte erarbeitet, die auf die Riemannsche Zetafunktion und die Riemannsche Vermutung hinarbeiten. Eine Auswahl der behandelten Themen in den Videos habe ich hier zusammengestellt:• Die Riemannsche Zetafunktion, Eulersche Produkte,• Partialbruchzerlegung der Cotangensfunktion,• Bernoullizahlen,• Gammafunktion und deren holomorphe als auch meromorphe Fortsetzung,• Euler-Mascheroni-Konstante,• Gaußsche Produktdarstellung der Gammafunktion,• Produktdarstellung der komplexen Sinusfunktion,• Verdoppelungsformel der Gammafunktion,• Integraldarstellung der Riemannschen Zetafunktion,• Meromorphe Fortsetzung der Riemannschen Zetafunktion,• Poissonsche Summenformel,• Theta-Reihe, Psi-Reihe,• Riemannschen Zetafunktion, Funktionalgleichung, triviale Nullstellen, kritischer Streifen,• Riemannsche Vermutung,• Primzahlsatz und Tschebyscheffsche Thetafunktion,• Tschebyscheffsche Phi-Funktion,• Taubersatz von Newmann und Korevaar,• Beweis des Primzahlsatzes,• Explizite Formel von Riemann für die Primzahlzählfunktion.
Ein weiteres wichtiges Teilgebiet, besonders für die Informatiker unter Ihnen, beschäftigt sich mit Fragestellungen aus der algebraischen Zahlentheorie. Dabei wird es im Wesentlichen um die Darstellung von Zahlen in beliebigen Basen gehen und wie man in solchen Basen die Grundrechenarten ausführen kann. Besprochen werden hier im Einzelnen insbesondere folgende Schwerpunkte:• Stellenwertsysteme,• g-adische Darstellung natürlicher, rationaler und reeller Zahlen,• g-adische Bruchentwicklung,• periodische g-adische Zahlen, Periodenlänge, Vorperiodenlänge,• algebraische Zahlen und Abzählbarkeit,• Transzendente Zahlen,• Transzendenzbeweis von Pi und der Eulerschen Zahl e,• Satz von Lindemann und Weierstraß,• Satz von Gelfond und Schneider,• algebraische Punkte,• Quadratur des Kreises.
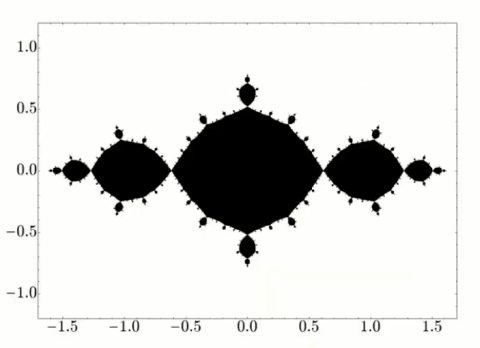
In dieser Rubrik Ausgewählte Kapitel der Mathematik soll auf einige interessante Fragen der fraktalen Geometrie näher eingegangen werden, die dem einem oder anderen Interessierten an die Grenzen seiner Vorstellungskraft bringen könnte.Beispielsweise kann man sich fragen, ob es im dreidimensionalen Raum Körper gibt, mit einem Volumen von null aber mit einer unendlich großen Oberfläche? Was würden Sie auf eine solche bizarre Frage eigentlich antworten? Der gesunde „Menschenverstand” sagt uns alle wahrscheinlich doch: So etwas kann es nicht geben! Sie werden hier aber sehen, dass solche und ähnliche Phänomene des öfteren auftreten können, wie beispielsweise im Paradoxon von Gabriels Horn. Auch muss bei solchen merkwürdigen Objekten der uns geläufige Dimensionsbegriff überarbeitet werden. Es wird gezeigt, dass hier geometrische Objekte mit einer gebrochenen, also nicht ganzzahligen, Dimension entstehen.Behandelt werden hier unter anderem folgende lehrreiche und interessante Beobachtungen:• Gabriels Horn bzw. Torricellis Trompete,• Menger-Schwamm,• Cantorstaub, Cantormenge,• Kochkurve, Kochsche Schneeflocke,• Sierpinski-Dreieck,• Hilbertkurve,• Dimensionsbegriff, Selbstähnlichkeitsdimension,• Fluchtmenge und Gefangenenmenge,• Julia-Mengen,• Mandelbrot-Menge,• Chaos, Newton-Fraktale.
In dieser Rubrik Ausgewählte Kapitel der Mathematik, möchte ich hier näher auf den abstrakten Begriff der Unendlichkeit eingehen, der für die meisten Menschen wohl eher fremd sein wird und oft vielleicht einfach mit der Unendlichkeit des Universums identifiziert wird.In dieser Videoserie wird es jetzt vor allem darum gehen, was man unter dem Begriff Unendlichkeit überhaupt zu verstehen hat und wie die Unendlichkeit insbesondere mathematisch definiert werden kann. Fragen wie, was ist unendlich klein oder was ist unendlich groß, stehen hier eigentlich nicht im Vordergrund, sondern vielmehr das Abzählen von Objekten, oder etwas mathematischer formuliert, das Abzählen von Elementen einer zuvor konkret definierten Menge. Diese Überlegungen gehen auf den genialen deutschen Mathematiker Georg Cantor zurück, der sich als erster mit derartigen Fragestellungen auseinandersetzte.Einen Überblick über die wichtigsten Themen die Sie hier erwarten dürfen:• Begriff der Unendlichkeit,• abzählbare Mengen. überabzählbare Mengen,• Cantors erstes und zweites Diagonalargument,• Mächtigkeit von abzählbaren unendlichen Mengen,• Aleph-Null,• Mächtigkeit von Potenzmengen endlicher Mengen,• Satz von Cantor,• Cantors Kontinumshypothese,• Hierachie der Alephs.
In dieser Rubrik Ausgewählte Kapitel der Mathematik, die sich mit den grundlegenden Methoden und Verfahren der Variationsrechnung beschäftigt, geht es im Wesentlichen darum, wie man Extrema von Funktionalen berechnen kann.In der Variationsrechnung werden also keine Punkte gesucht, wie zum Beispiel in der reellen Analysis üblich, wo Punkte gesucht werden die einen Funktionswert maximieren oder auch minimieren sollen, sondern es werden hier jetzt Funktionen gesucht, die einen bestimmten Ausdruck, meist einen integralen Ausdruck, extremal machen sollen. Das wohl bekannteste Problem ist das sogenannte Brachystochronenproblem, mit dem sich schon der Mathematiker Bernoulli ausgiebig beschäftigt hatte.Aufgrund der großen Reichweite gehört die Variationsrechnung nicht nur in der theoretischen Physik sondern auch in einigen ingenieurwissenschaftlichen Studiengängen heute zum mathematischen „Knowhow” und sollte daher auch beherscht werden.Eine Übersicht der einzelnen vorgetragenden Themenkomplexe die Sie erwartet, finden Sie hier:• Funktionale, Funktionalmathematik,• Euler-Lagrange-Gleichung,• Cantorstaub, Cantormenge,• Brachystochronenproblem,• verallgemeinerte Euler-Lagrange-Gleichung,• zweite Variation,• Legendre-Bedingung,• konvexe Mengen,• konvexe Funktionen, konkave Funktionen,• Konvexität differenzierbarer Funktionen,• Funktionale mit konvexen Integranden.
Tensorrechnung
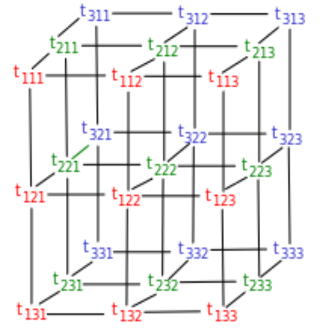
In dieser Rubrik Ausgewählte Kapitel der Mathematik soll eine erste grundlegende Einführung in das anspruchsvolle Gebiet der Tensorrechnung vermittelt werden. Die Tensorrechnung spielt nicht nur in der theoretischen Physik, wie z.B. in der speziellen und allgemeinen Relativitätstheorie eine zentrale Rolle, sondern auch in einigen Ingenieurbereichen, wie beispielsweise in der technischen Mechanik oder der angewandten Elektrodynamik. Grundsätzlich lassen sich einige Teile der Tensorrechnung in das umfangreiche Gebiet der Linearen Algebra einordnen und andere Teile wiederum in das Gebiet der sehr anspruchsvollen Differentialgeometrie, was aber aus Zeitgründen oft nicht in diesen Veranstaltungen integriert wird und daher in der Regel einer separaten Vorlesung vorbehalten ist.Zu der hier präsentierten Themenauswahl, die sich in die Lineare Algebra eingliedern lässt, gehören:• Was ist überhaupt Tensorrechnung?• Einsteinsche Summenkonvention,• kovariante und kontravariante Größen,• Matrix der Metrikkoeffizienten, Metriktensor,• duale Vektorbasen, kontravariante Basen,• kovariante und kontravariante Vektorkomponenten,• Basistransformationen,• Tensoren erster, zweiter und höherer Stufe,• Transformation kovarianter und kontravarianter Größen,• Tensoralgebra,• antisymmetrische Tensoren,• Levi-Civita-Symbol,• Epsilon-Tensor,• Rechtssysteme und Linkssysteme,• Pseudotensoren, Polarvektoren, Axialvektoren,• vektorielles Produkt und höhere vektorielle Produkte.
Fragen, wie zum Beispiel was ist ein flacher oder gekrümmter Raum, fallen in das große und auch sehr anspruchsvolle Gebiet der Differentialgeometrie. Nicht nur in der allgemeinen Relativitätstheorie spielen differentialgeometrische Konzepte eine wichtige Rolle, sondern auch in einigen Bereichen der Naturwissenschaften. Behandelt werden hier unter anderem folgende Themen:• Mannigfaltigkeiten und Untermannigfaltigkeiten,• Koordinatentransformationen,• Koordinatensysteme, Koordinatenlinien, Koordinatenflächen, krummlinige Koordinaten,• lokale und globale kovariante und kontravariante Vektorbasen,• Transformation von Vektorbasen bei Koordinatentransformation,• Transformation von Tensoren bei Koordinatentransformation,• Differentiation von Tensorfeldern,• Christoffelsymbole erster und zweiter Art,• kovariante Ableitung und deren Rechenregeln,• Differentialoperatoren in krummlinigen Koordinaten,• Theorem von Ricci,• Quotiententheorem,• Riemannscher Krümmungstensor,• Bogenlängen auf Mannigfaltigkeiten,• euklidische und nichteuklidische Geometrie,• Riemannsche Räume,• Normalkrümmung und geodätische Krümmung,• Differenzialgleichung der geodätischen Linie,• Variationsprinzip und extremale Kurven,• Raumkrümmung,• Paralleltransport von Vektoren.
Klassische Algebra
Polynomiale Gleichungen und Gleichungssysteme 1 - 24
Polynomiale Gleichungen und Gleichungssysteme 1 - 24

In dieser Rubrik Ausgewählte Kapitel der Mathematik werde ich Ihnen verschiedene Methoden und Verfahren, zur exakten als auch zur numerischen Lösung von nichtlinearen Gleichungen und nichtlinearen Gleichungssystemen, vorstellen.Die klassische Algebra kann, etwas vereinfacht gesagt, historisch als die Lehre vom Lösen von Gleichungen verstanden werden. Dagegen befasst sich die heutige moderne abstrakte Algebra mit zusätzlichen darüber hinausgehenden algebraischen Strukturen wie zum Beispiel Gruppen, Ringen, Körpern und sogenannten Körpererweiterungen. Ich werde mich hier allerdings nur auf diejenigen Zusammenhänge beschränken, die für den in der Praxis stehenden Ingenieur von Bedeutung sind und nicht etwa auf die Galoistheorie eingehen, da diese keinen praktischen Nutzen nach sich zieht .In dieser Videoreihe zur klassischen Algebra sollen die grundlegenden Lösungsstrategien solcher Gleichungen entwickelt werden, die ein Ingenieur zumindest einmal gesehen haben, ja wenn nicht sogar beherrschen sollte.Zum exakten Lösen solcher Gleichungen beziehungsweise Gleichungssystemen werden die folgenden Kapitel erarbeitet:• Polynomiale Gleichungen,• Fundamentalsatz der Algebra,• kubische Gleichungen und Cardanische Formeln,• komplexe Wurzeln und primitive Einheitswurzel,• quartische Gleichungen und seine kubische Resolvente,• quintische Gleichungen,• Substitutionsmethoden für polynomiale Gleichungen,• Exponentialgleichungen mit trigonometrischen Funktionen,• kubische und quartische trigonometrische Gleichungen,• polynomiale Gleichungssysteme,• symmetrische nichtlineare Gleichungssysteme,• Lambertsche W-Funktion,• unendliche Potenztürme,• Potenzturmfunktion und seine Umkehrfunktion,• Potenzturmgleichungen.
Weil sich ja bekanntlich die meisten Gleichungen und Gleichungssysteme nicht auf konventionellen algebraischen Wegen auflösen lassen, werde ich in den folgenden Videos die grundlegenden numerischen Lösungsstrategien vorstellen, um solche, zumindest numerisch mit einer akzeptalen Genauigkeit zu Lösen. Sie finden hier folgende Verfahren vorgetragen:• Fixpunktsatz und Stabilität der Fixpunkte,• Bisektionsverfahren,• Regula-Falsi-Verfahren,• Sekantenverfahren,• Newton-Raphson-Verfahren,• Newton-Verfahren für nichtlineare höherdimensionale Gleichungssysteme.
Numerische Methoden
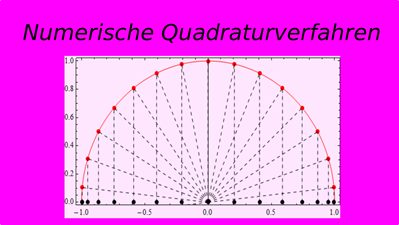
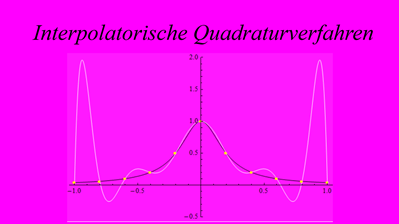
In dieser Rubrik Ausgewählte Kapitel der Mathematik werden einige der gängigen Verfahren zur numerischen Lösung von bestimmten Integralen und gewöhnlichen Differenzialgleichungen ausführlich behandelt. Da allgemein bekannt sein sollte, dass es nur in ganz wenigen speziellen Ausnahmefällen möglich ist, die in der Praxis auftretenden Integrale und erst recht Differenzialgleichungen exakt zu lösen, benötigt der Ingenieur ein geeignetes sicheres Hilfsmittel, um solche Probleme zumindest näherungsweise in den Griff zu bekommen.Zur approximativen numerischen Auswertung von bestimmten Integralen werden hier die folgende Verfahren behandelt:• Elementare Quadraturverfahren,• zusammengesetzte Trapezformel und zusammengesetzte Simpsonformel,• Polynominterpolation, Lagrange-Polynome, Newton-Polynome,• Tschebyscheff-Polynome,• Spline-Interpolation,• konstruktion von kubischen Splines,• interpolatorische Quadraturformeln von Newton und Cotes,• stückweise interpolatorische Quadratur,• uneigentliche Integrale,• Gauß-Quadratur,• Orthogonalisierungsverfahren von Gram-Schmidt,• Orthogonalpolynome„• Legendre-Polynome, Tschebyscheff-Polynome, Laguerre-Polynome, Hermite-Polynome,• Gauß-Legendre-Quadratur, Gauß-Laguerre-Quadratur, Gauß-Hermite-Quadratur.